 中学生
中学生
こんにちは、中学生専門・伸び悩み解消学習コーチの久松隆一です。
今日は「数学を解いているときに、途中で解き方が分からなくなる」原因と解決策について。
よく「途中で解き方が分からなくなる…」という相談をいただきます。
実際に授業をしていても、数え切れないほどそんな場面に遭遇します。
ほんと、誰にでも起こります。
習ったばかりの単元は特にそうですね。
しかし、問題数をこなしていくうちに、このカベを乗り越えていく人もいれば、なかなかこのカベ超えられない人もいます。
この違いは、実は普段の勉強の仕方に原因があります。
普段から「解き方が分からなくなる」ことがよく起こる人は、テスト本番になると「急に頭が真っ白になった」という人も少なくありません。
これは、実際は「急に頭が真っ白になった」のではなくて、
勉強の段階で「途中で解き方が分からなくなってしまう」ような勉強の仕方をしているのです。
というわけで、今日は数学の問題を解いているとき、途中で解き方が分からなくなってしまう原因と解決策について解説します。
なぜ途中で解き方が分からなくなるのか?
途中で解き方が分からなくなる原因は、一言で言えば、
「頭の中で、解き方がごちゃごちゃになってしまうから」
数学の問題には、解き方の手順があります。
料理で言えばレシピですね。
どんな料理にもレシピがあるように、どんな数学の問題にもレシピがあります。
頭の中で、このレシピがごちゃごちゃになってしまうから、途中で解き方が分からなくなってしまうのです。

カレーライスであれば、こんな感じのレシピになりますね。
(引用元:ハウス食品 https://housefoods.jp/recipe/rcp_00012871.html)
- 材料を切る
- 材料を炒める
- 水を加えて煮込む
- ルウを溶かしてさらに煮込む
こんな手順になっていますね。
・・・ちょっと想像してみてください。
もし、あなたがカレーを作っているとき、この手順が頭の中でごちゃごちゃになって、材料を切る前に丸ごと煮込んだら・・・笑
食べたくないですよね。笑
数学の問題にも同じようにレシピがあります。
習いたての料理はレシピを見ながらじゃないと作れないのと同じで、数学の問題を解く場合も、習いたての頃は解き方の手順があやふやなまま。
だから解けないし、途中で解き方が分からなくなってしまうのです。
仮にレシピを覚えていたとしても、レシピが複雑なので、途中で頭が混乱してしまうこともある。
こうして、解き方が途中で分からなくなってしまうわけです。
となると、この解決策は「解き方の手順をしっかり整理する」ことです。
以下では、解き方の手順を整理する方法を紹介します。
「途中で解き方が分からなくなる問題」を解消する3ステップ
大きく3つのステップに分かれます。
- ゴールを考える
- ゴールを求めるために、必要な情報は何か?考える
- 一つずつ必要な情報を揃える
この3ステップです。
これだけだと何を言ってるか分からないと思うので、実際に一次関数の問題を例に見ていきましょう。
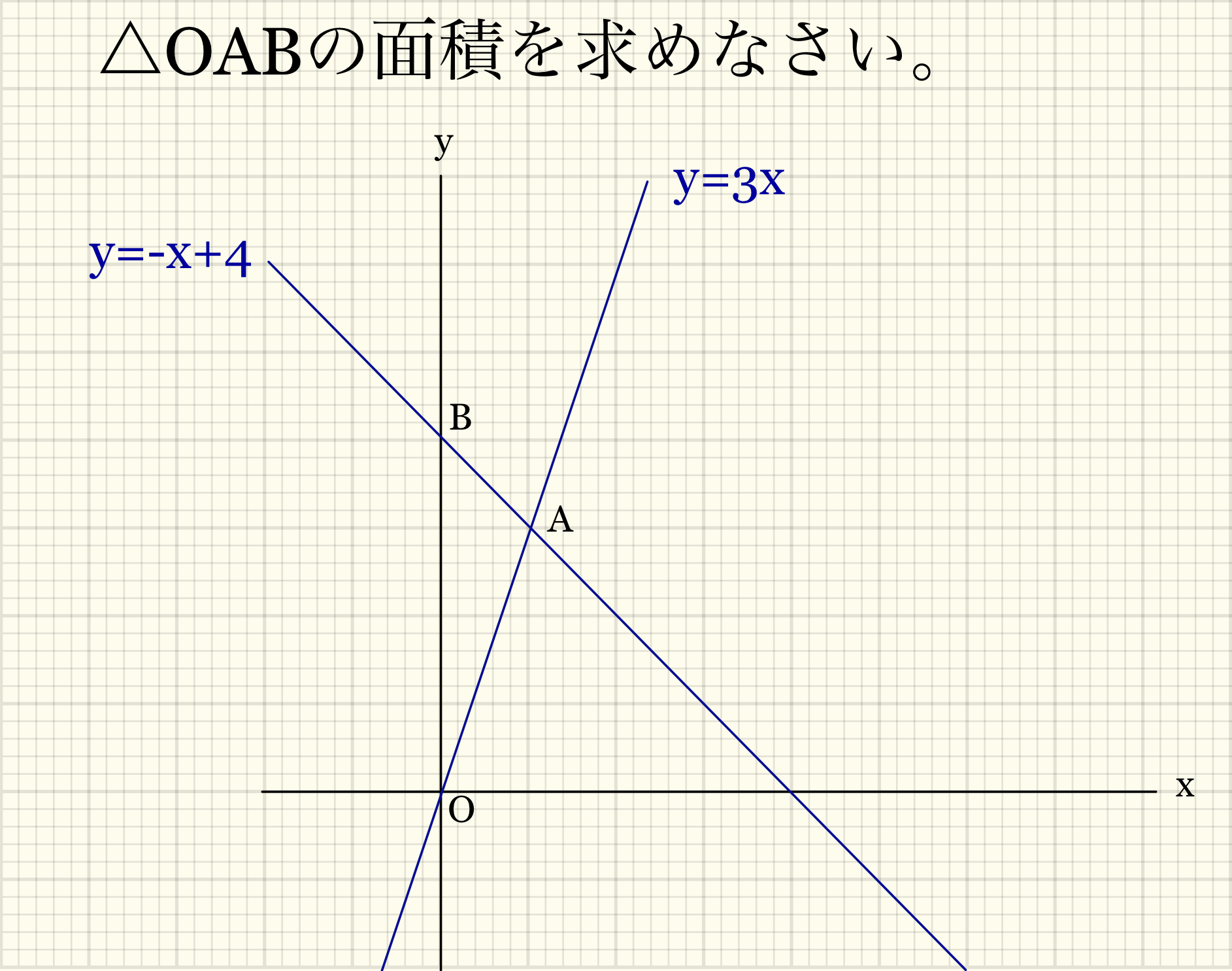
まず問題はこちら
△OABの面積を求める問題です。

ステップ1:ゴールを考える
最初の手順はゴールを考えることです。
そもそもゴールとは「この問題で何を聞かれているのか?」です。
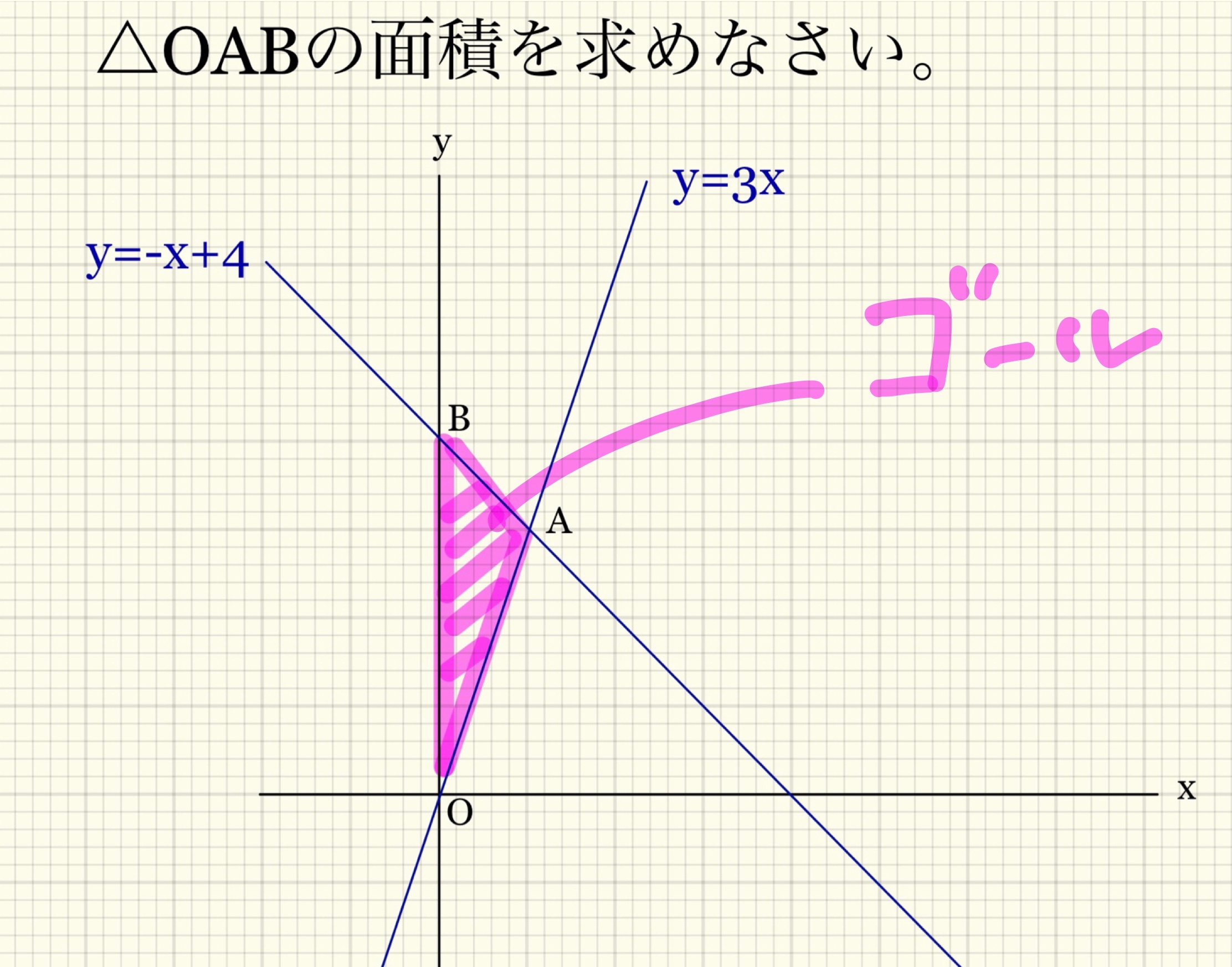
では、この問題のゴールは何でしょうか?
この問題では、三角形の面積を聞かれていますよね?
これがゴールです。

ステップ1では、
「この問題では何を聞かれているんだろう?」
と考えてみてください。
途中で解き方が分からなくなる人は、「まず何を計算したらいいんだろう?」と考える傾向があります。
そうではなく、「ゴールはなんだろう?」から思考をスタートさせてください。
ステップ2:ゴールを求めるために必要な情報は何か?考える
続いてステップ2では、必要な情報は何か?と考えることです。
ゴールは三角形の面積を求めること。
なので、次は「三角形の面積を求めるために必要なものは何だろう?」と考えてください。
三角形の面積は、
で求められますよね?
なので、ゴールを求めるために必要な情報は「底辺」と「高さ」になります。

さらに、
- 「底辺」を求めるために必要な情報は何だろう?
- 「高さ」を求めるために必要な情報は何だろう?
と考えます。
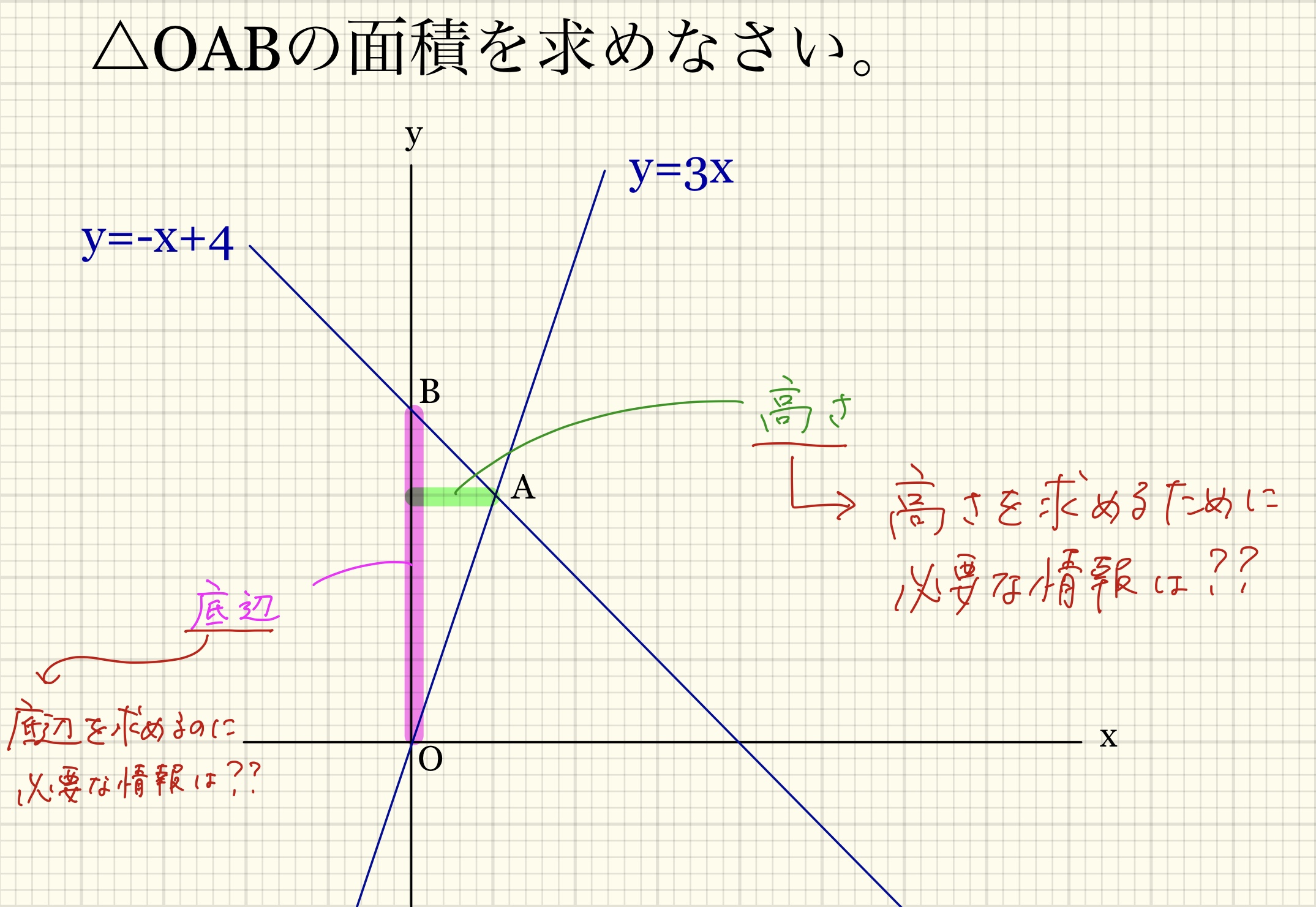
あとはこの作業の繰り返しです。「○○を求めるために必要な情報は何だろう?」を繰り返していきましょう。
これがステップ2です。
ステップ3:必要な情報を揃える
最後はステップ3。
「必要な情報は何だろう?」と繰り返していくと、どこかで問題文から必要な情報が揃います。
必ずです。
必ずどこかで問題文から読み取れます。
(数学の問題はそのようにできています)
解説は省略しますが、問題文から
点Aの座標は(3,1)
点Bの座標は(0,4)
と求められます。
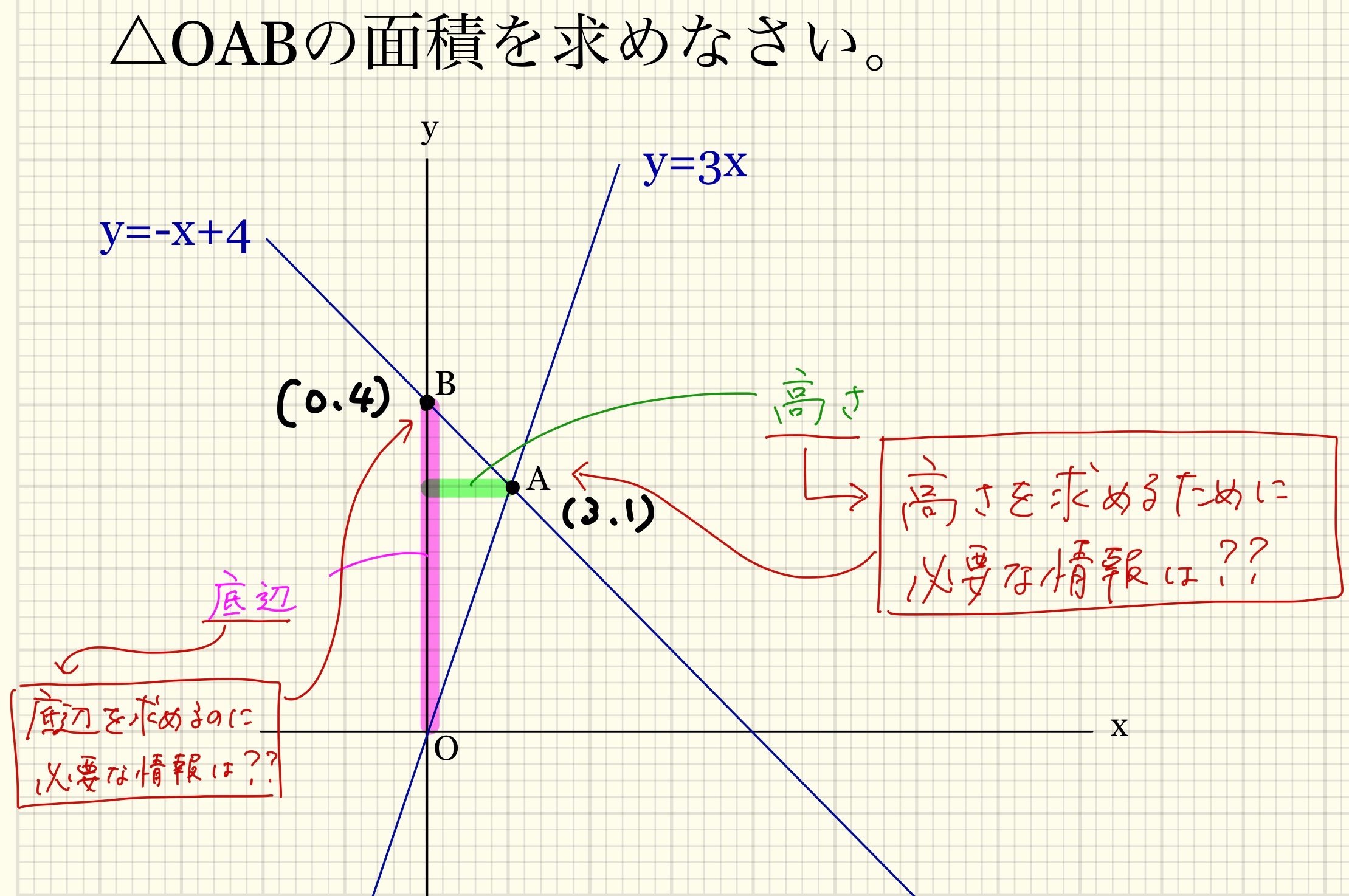
ここまで来れば、あとは、
座標が分かる
↓
底辺と高さが分かる
↓
三角形の面積が分かる
という具合に、ステップ2までで進んできた道を後戻りするだけです。
こうすれば、一度来た道を戻るだけなので、もう迷わないですよね。
途中で解き方が分からなくなることもありません。
実は数学が得意な人は、当たり前のようにこんな思考回路で解いています。
まずゴールを考えて、そこから必要な情報を逆算していく。
必要な情報が揃ったら、ゴールに向けて今来た道を戻る。
だから途中で解き方が分からなくなるなんてことは起こらない。
スラスラ問題が解けるようになるし、点数も取れる。
たったそれだけのことなんですね、頭が良いとか悪いとか関係ないんです。
勉強の仕方です。
まとめ
数学の問題で途中で解き方が分からなくなる場合は、普段の勉強から「ゴールから逆算する」思考回路で数学の問題を解く練習をしてみてください。
この勉強の仕方を実践していれば、途中で解き方が分からなくなることも、テストで急に頭が真っ白になることもなくなります。
当たり前ですが、点数も伸びてきます。
さぁ、あとは普段から意識してやるだけ!
日々、ゴールから逆算する思考回路で問題を解く練習を積んでいきましょう!
なお、数学の点数が伸びる人と伸びない人の勉強法の違いについては、こちらにまとめてありますので、よければ参考にしてみてください!




